Stabilité & Formule de Miller
5 participants
:: Le club-house :: La bibliothèque
Page 1 sur 1
 Stabilité & Formule de Miller
Stabilité & Formule de Miller
Voila la formule dans sa forme de base:
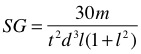
SG = coefficient de stabilité Miller
m = masse du projectile en grains
t = pas du canon exprimé en calibres par tour
d = le diamètre (calibre) du projectile en pouces
l = longueur du projectile exprimé en calibres
Cette formule est une avancée dans le calcul des projectiles stabilisées par rotation (2005). Avant il n'y avait que la formule de Greenhill qui était destiné aux projectiles sphériques.
Exemple: considérons un projectile de 0.308 avec un poids de 155 grains qui mesure 1.2" de long et qui est tiré d'un canon avec un pas de 13", Quel est le coef de stabilité?
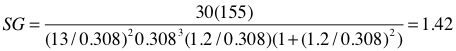
ou en format tableur (Excel):
SG=(30*155)/((13/.308)^2*.308^3*1.2/.308*(1+(1.2/.308)^2))
Dans cette exemple le facteur de stabilité est de 1.42 ce qui est supérieur à la valeur empirique de 1.4 en dessous duquel il vaut mieux ne pas descendre, bien que SG>=1 devrait suffire. Les benchrester vont plutôt taquiner du 1.2 car une sur-stabilisation a d'autres inconvénients; celle de faire augmenter la dispersion par des défauts de concentricité, qui elle sera amplifiée au plus grande est la vitesse gyroscopique du projectile.
Si nous analysons la formule, on voit que la stabilité augmentera proportionnellement avec la masse du projectile; pour un calibre donné la stabilité sera divisé (1) du pas du canon (pas plus lent = moins stable) et (2) par la longueur du projectile (plus long moins stable). De la aussi, un projectile plus lourd sera forcément plus long (en supposant la même matière) et demandera un pas plus serré pour être stabilisé.
La formule peut être écrite dans une forme plus étendue en tenant compte de la vitesse du projectile et de la pression atmosphérique et température (densité de l'air):
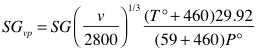
v = vitesse en pieds seconde
T° = température en Fahrenheit
P° = pression atmosphérique en pouces de mercure
dans un exemple ou la V0 est de 3000 pieds/s et la pression 28.50 inchHg et température 85°F ça donne ça:
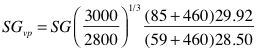
ce qui donne 1.42 * 1.023 * 1.10 = 1.60
une plus haute vitesse donne un meilleure stabilité (2800 pieds/sec est la base de référence pour la formule de Miller), une densité d'air moins élevée l'améliore aussi.
PS. j'ai un tableur ou tout est converti en unités métriques, mais je n'ai pas eu le courage de le transposer ici (ferai plus tard)
Ref: Applied Ballistics for Long Rang Shooting (Bryan Litz, 2009)
Formulas by MathType for Word 2011 for Mac
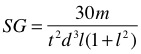
SG = coefficient de stabilité Miller
m = masse du projectile en grains
t = pas du canon exprimé en calibres par tour
d = le diamètre (calibre) du projectile en pouces
l = longueur du projectile exprimé en calibres
Cette formule est une avancée dans le calcul des projectiles stabilisées par rotation (2005). Avant il n'y avait que la formule de Greenhill qui était destiné aux projectiles sphériques.
Exemple: considérons un projectile de 0.308 avec un poids de 155 grains qui mesure 1.2" de long et qui est tiré d'un canon avec un pas de 13", Quel est le coef de stabilité?
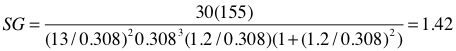
ou en format tableur (Excel):
SG=(30*155)/((13/.308)^2*.308^3*1.2/.308*(1+(1.2/.308)^2))
Dans cette exemple le facteur de stabilité est de 1.42 ce qui est supérieur à la valeur empirique de 1.4 en dessous duquel il vaut mieux ne pas descendre, bien que SG>=1 devrait suffire. Les benchrester vont plutôt taquiner du 1.2 car une sur-stabilisation a d'autres inconvénients; celle de faire augmenter la dispersion par des défauts de concentricité, qui elle sera amplifiée au plus grande est la vitesse gyroscopique du projectile.
Si nous analysons la formule, on voit que la stabilité augmentera proportionnellement avec la masse du projectile; pour un calibre donné la stabilité sera divisé (1) du pas du canon (pas plus lent = moins stable) et (2) par la longueur du projectile (plus long moins stable). De la aussi, un projectile plus lourd sera forcément plus long (en supposant la même matière) et demandera un pas plus serré pour être stabilisé.
La formule peut être écrite dans une forme plus étendue en tenant compte de la vitesse du projectile et de la pression atmosphérique et température (densité de l'air):
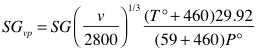
v = vitesse en pieds seconde
T° = température en Fahrenheit
P° = pression atmosphérique en pouces de mercure
dans un exemple ou la V0 est de 3000 pieds/s et la pression 28.50 inchHg et température 85°F ça donne ça:
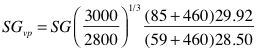
ce qui donne 1.42 * 1.023 * 1.10 = 1.60
une plus haute vitesse donne un meilleure stabilité (2800 pieds/sec est la base de référence pour la formule de Miller), une densité d'air moins élevée l'améliore aussi.
PS. j'ai un tableur ou tout est converti en unités métriques, mais je n'ai pas eu le courage de le transposer ici (ferai plus tard)
Ref: Applied Ballistics for Long Rang Shooting (Bryan Litz, 2009)
Formulas by MathType for Word 2011 for Mac
Dernière édition par Darius le Ven 27 Jan 2012 - 10:03, édité 1 fois (Raison : typo erreur)
 Re: Stabilité & Formule de Miller
Re: Stabilité & Formule de Miller
Un grand merci pour ce post, hop c'est ajouté dans mes docs ! 
N'y connaissant strictement rien en TLD, et en admettant que tu partes de rien :
Combien de calculs différents sont ils nécessaires pour un tir ?
Coeff de Miller, un autre pour connaitre le nombre de clics j'imagine, ... ?
N'y connaissant strictement rien en TLD, et en admettant que tu partes de rien :
Combien de calculs différents sont ils nécessaires pour un tir ?
Coeff de Miller, un autre pour connaitre le nombre de clics j'imagine, ... ?

Rob1- hors classe

- Nombre de messages : 5560
Age : 35
Localisation : Isère
Date d'inscription : 18/08/2011
 Re: Stabilité & Formule de Miller
Re: Stabilité & Formule de Miller
Non, ce calcul ne se fait pas au moment u tir. Eventuellement, lors d'une sélection de couple arme, munition, ou lors d'une conception de projectile. Le calcul lors du tir ce fait au moyen de tables ou d'un calculateur; ce calcul tient compte de la distance, le vent (force & direction) la déclivité (cible se trouvant plus haut, plus bas), la densité de l'air (température, pression, altitude); vitesse / cap de la cible; cette table a comme variables primairesä: la V0 (vitesse initiale), coefficient balistiques du projectile et le parallaxe (entre-axe canon / lunette). Les éléments à reporter sont une hausse (haut/bas) et une dérive (gauche droite). A partir de 500m le calcul incorpore aussi les éléments tels que la dérive gyroscopique et à partir de 1000m les forces de Coriolis (pour cette dernière. il faudra introduire la latitude de la position et la direction / cap du tir).
 Re: Stabilité & Formule de Miller
Re: Stabilité & Formule de Miller
le coef SG pondéré par la vitesse et la pression, quel est sa valeur idéale? et l'intervalle de confiance?
D'un point de vue dimension (mathématique), l'unité de mesure de ce coefficient est particulièrement aberrant...
si de manière empirique il est possible de donner une signification à un ratio dont la cohérence dimentionelle est dicutable, il est nécessaire de préciser l'intervalle dans lequel il est significatif...
D'un point de vue dimension (mathématique), l'unité de mesure de ce coefficient est particulièrement aberrant...
si de manière empirique il est possible de donner une signification à un ratio dont la cohérence dimentionelle est dicutable, il est nécessaire de préciser l'intervalle dans lequel il est significatif...

Marcaurel- modo
- Nombre de messages : 6271
Age : 47
Localisation : Helvético-Arverne
Emploi : Apothicaire
Date d'inscription : 25/07/2008
 Re: Stabilité & Formule de Miller
Re: Stabilité & Formule de Miller
Tu oublies que tu peux aussi donner des dimensions opposées à une constante, qui de ce fait annulerait les dimensions des autre facteurs, rendant ainsi le résultat sans dimensions. Vu le point qui précède, le deuxième point n'a plus lieu d'être 

 Re: Stabilité & Formule de Miller
Re: Stabilité & Formule de Miller
une constante est une constante, pas une variable...
 je ne vois que des variables (sauf le "30") et une constante doit être definie comme tel
je ne vois que des variables (sauf le "30") et une constante doit être definie comme tel
Et si tu ne peux me donner un intervalle (ou seuils de la valeurs) ayant une réelle signification pour SG, la description que tu en a fait (toi ou la "source") me parait quand même pas des masses "rigoureuse":
Enfin malgré tout c'est intéressant, ça permet de voir les facteur influençant la stabilisation ...
 je ne vois que des variables (sauf le "30") et une constante doit être definie comme tel
je ne vois que des variables (sauf le "30") et une constante doit être definie comme telEt si tu ne peux me donner un intervalle (ou seuils de la valeurs) ayant une réelle signification pour SG, la description que tu en a fait (toi ou la "source") me parait quand même pas des masses "rigoureuse":
Dans cette exemple le facteur de stabilité est de 1.42 ce qui est supérieur à la valeur empirique de 1.4 en dessous duquel il vaut mieux ne pas descendre, bien que SG>=1 devrait suffire. Les benchrester vont plutôt taquiner du 1.2 car une sur-stabilisation a d'autres inconvénients
Enfin malgré tout c'est intéressant, ça permet de voir les facteur influençant la stabilisation ...

Marcaurel- modo
- Nombre de messages : 6271
Age : 47
Localisation : Helvético-Arverne
Emploi : Apothicaire
Date d'inscription : 25/07/2008

Gavrinis- general

- Nombre de messages : 2199
Age : 74
Localisation : dans le courant
Date d'inscription : 24/03/2011
 Re: Stabilité & Formule de Miller
Re: Stabilité & Formule de Miller
Tu veux que je te la fasse "scientifique" façon New Scientist ? Ici ce qui nous intéresse c'est de mettre en équation les interactions des éléments qu'il est intuitivement facile de comprendre: vitesse, masse et longueur du projectile; pas du canon; densité de l'air.
Tu est tombé sur ton vieux cours de physique de 1ère année de fac ou est-ce tu t'es fâché avec madame, ce matin?
Pour l'analyse et la démonstration complète, je te réfère au "Modern Exterior Ballistics" de Robert Mc Coy, page 209 à 211.
Pour te répondre à ta question: à usage militaire: entre 1.4 et 2; pour les benchresters le plus près de 1 (disons 1.2) tout en laissant de la marge pour faire face à toute variation des facteurs car en dessous de 1, même de façon minimale, le projectile culbute,
Tu est tombé sur ton vieux cours de physique de 1ère année de fac ou est-ce tu t'es fâché avec madame, ce matin?
Pour l'analyse et la démonstration complète, je te réfère au "Modern Exterior Ballistics" de Robert Mc Coy, page 209 à 211.
Pour te répondre à ta question: à usage militaire: entre 1.4 et 2; pour les benchresters le plus près de 1 (disons 1.2) tout en laissant de la marge pour faire face à toute variation des facteurs car en dessous de 1, même de façon minimale, le projectile culbute,
Dernière édition par Darius le Ven 27 Jan 2012 - 10:21, édité 1 fois
 Re: Stabilité & Formule de Miller
Re: Stabilité & Formule de Miller
je te taquine Darius, te faches pas,
et c'est vrai que je voulais faire de la intelectuelle...rien que la formule de début fait peur au premier abors
intelectuelle...rien que la formule de début fait peur au premier abors 
je vais faire quelques calculs avec differents calibres !
ah ouais, mais non, je connais pas les longueurs d'ogive
ça donne quoi le couple GP11/K31 et GP90/fass90 par exemple
La longueur du canon n'a aucune influence? (ben si, la vitesse)
EN tout cas, c'est trop compliqué pour moi d’emblée, j'aimerais beaucoup lire les 21 première pages de son livre qui , je crois, retrace l'histoire de la balistique, j'imagine que ça me permettrait d'acquerir la culture et les clefs de la compréhension de cette science empirique!
et c'est vrai que je voulais faire de la
 intelectuelle...rien que la formule de début fait peur au premier abors
intelectuelle...rien que la formule de début fait peur au premier abors je vais faire quelques calculs avec differents calibres !
ah ouais, mais non, je connais pas les longueurs d'ogive

ça donne quoi le couple GP11/K31 et GP90/fass90 par exemple
La longueur du canon n'a aucune influence? (ben si, la vitesse)
EN tout cas, c'est trop compliqué pour moi d’emblée, j'aimerais beaucoup lire les 21 première pages de son livre qui , je crois, retrace l'histoire de la balistique, j'imagine que ça me permettrait d'acquerir la culture et les clefs de la compréhension de cette science empirique!

Marcaurel- modo
- Nombre de messages : 6271
Age : 47
Localisation : Helvético-Arverne
Emploi : Apothicaire
Date d'inscription : 25/07/2008
 Re: Stabilité & Formule de Miller
Re: Stabilité & Formule de Miller
Le bouquin de McCoy, je devrai dire "à l'honneur de McCoy" car ce sont ses élèves qui l'ont compilé, demande une très bonne connaissance de mathématiques supérieures. C'est très ardu à lire et comprendre, mais c'est l'approche scientifique pure et dure.
Je te conseille vivement le bouquin de Bryan Litz (que l'ai rencontré à Vegas au stand de Berger) qui est juste le bon niveau de vulgarisation pour rester compréhensible (bon, il faut quand-même une base scientifique) sans aller dans la vulgarisation. Ce dernier est un "must have" pour tout le monde qui s'intéresse au TLD, voir balistique extérieure. (Applied Ballistics for Long Range Shooting). Le bouquin comprend une multitude de données mesurées sur un large éventail de calibres, dont le coefficient balistique. Cette dernière relevant, le plus souvent, de la plus haute fantaisie de la part des munitionnaires...
http://www.appliedballisticsllc.com/Products.htm

Je te conseille vivement le bouquin de Bryan Litz (que l'ai rencontré à Vegas au stand de Berger) qui est juste le bon niveau de vulgarisation pour rester compréhensible (bon, il faut quand-même une base scientifique) sans aller dans la vulgarisation. Ce dernier est un "must have" pour tout le monde qui s'intéresse au TLD, voir balistique extérieure. (Applied Ballistics for Long Range Shooting). Le bouquin comprend une multitude de données mesurées sur un large éventail de calibres, dont le coefficient balistique. Cette dernière relevant, le plus souvent, de la plus haute fantaisie de la part des munitionnaires...
http://www.appliedballisticsllc.com/Products.htm

 Re: Stabilité & Formule de Miller
Re: Stabilité & Formule de Miller
Darius a écrit:Non, ce calcul ne se fait pas au moment u tir. Eventuellement, lors d'une sélection de couple arme, munition, ou lors d'une conception de projectile.
J'avais compris qu'il s'agissait de choisir le type de projectile, d'où mon "en admettant que tu partes de rien".
Donc choix du projectile, tables de rechargement avant le tir.
Une fois sur le terrain c'est mesure des différents éléments (température etc) puis tu te réfère à tes "i-tables" ?
En tout cas merci pour les infos, pour le bouquin tout est en anglais ?

Rob1- hors classe

- Nombre de messages : 5560
Age : 35
Localisation : Isère
Date d'inscription : 18/08/2011
 Re: Stabilité & Formule de Miller
Re: Stabilité & Formule de Miller
Merci, très intéressant ce sujet !
Marcaurel : Il faut pas chercher à faire une analyse dimensionnelle sur une formule empirique, qui par définition est un modèle établi à partir de mesures et non d'une démonstration mathématique rigoureuse.
Il y a un calculateur disponible en ligne (qui heureusement donne le même résultat, mais attention aux unités !) :
http://www.jbmballistics.com/cgi-bin/jbmstab-5.1.cgi
Vous dites que greenhill n'est applicable que pour les projectiles sphériques, mais dans la formule que j'ai, la longueur intervient pour déterminer le pas :

J'ai lu je ne sais plus où que la formule était valable pour un projo en plomb, le terme (racine de rho / 10,5) a été ajouté ultérieurement pour faire une correction de densité. Il me semblait donc que ceci avait été établit vers le milieux du XIXème, conjointement au développement des balles minié/coniques.
Edit : Rob1 : Je vais paraphraser Darius en disant que tout ceci n'a que peu d'intérêt pour le tireur, Miller ne sert qu'à vérifier la compatibilité entre un projectile et le pas du canon. Les corrections au moment du tir (effet du vent, dérive gyroscopique...) n'ont rien à voir avec ça, sauf le coefficient balistique.
Parmi les autres résultats, je ne vois pas la différence entre votre i7 et ce qu'on appelle ailleurs G7 qui est un rapport d'une donnée aérodynamique de notre balle avec celle d'une balle de référence si j'ai bien compris.
J'ai vu aussi qu'on utilise rapport Rt/R (rayons de courbure ?) qui indique "comment" la balle est pointue.
http://www.appliedballisticsllc.com/index_files/Lapua_Scenar.pdf
J'aimerais bien jeter un oeil au bouquin que vous citez, mais le problème avec l'anglais, c'est que je suis jamais sûr d'avoir compris comme il faut ce qui est raconté...
Marcaurel : Il faut pas chercher à faire une analyse dimensionnelle sur une formule empirique, qui par définition est un modèle établi à partir de mesures et non d'une démonstration mathématique rigoureuse.
Il y a un calculateur disponible en ligne (qui heureusement donne le même résultat, mais attention aux unités !) :
http://www.jbmballistics.com/cgi-bin/jbmstab-5.1.cgi
Vous dites que greenhill n'est applicable que pour les projectiles sphériques, mais dans la formule que j'ai, la longueur intervient pour déterminer le pas :

J'ai lu je ne sais plus où que la formule était valable pour un projo en plomb, le terme (racine de rho / 10,5) a été ajouté ultérieurement pour faire une correction de densité. Il me semblait donc que ceci avait été établit vers le milieux du XIXème, conjointement au développement des balles minié/coniques.
Edit : Rob1 : Je vais paraphraser Darius en disant que tout ceci n'a que peu d'intérêt pour le tireur, Miller ne sert qu'à vérifier la compatibilité entre un projectile et le pas du canon. Les corrections au moment du tir (effet du vent, dérive gyroscopique...) n'ont rien à voir avec ça, sauf le coefficient balistique.
Parmi les autres résultats, je ne vois pas la différence entre votre i7 et ce qu'on appelle ailleurs G7 qui est un rapport d'une donnée aérodynamique de notre balle avec celle d'une balle de référence si j'ai bien compris.
J'ai vu aussi qu'on utilise rapport Rt/R (rayons de courbure ?) qui indique "comment" la balle est pointue.
http://www.appliedballisticsllc.com/index_files/Lapua_Scenar.pdf
J'aimerais bien jeter un oeil au bouquin que vous citez, mais le problème avec l'anglais, c'est que je suis jamais sûr d'avoir compris comme il faut ce qui est raconté...

Sulfat- hors classe

- Nombre de messages : 6063
Date d'inscription : 30/11/2011
 Re: Stabilité & Formule de Miller
Re: Stabilité & Formule de Miller
Je te la fais courte: les courbes balistiques ont été standardisées vu l'investissement assez considérable qu'il fallait faire pour les analyser et les mettre en place: le G est pour Gavres, qui tire son nom du Polygone de Gavres où les premiers calculs balistiques sérieux ont été effectués. On a essayé de faire plusieurs catégories de courbes balistiques, le tout corrigé avec un coefficient, en fonction de leur profil. Bon, le profil du G1 correspond au fameux obus de 75, assez fort éloigné des projectiles profilés qu'on utilise dans le tir. Le G7 correspond très bien à ce qu'on utilise. Le "problème" c'est que si on exprime un coef en fonction du profil G7 ça donne un chiffre beaucoup plus bas (le projectile de référence étant plus performant), donc ça déplait au munitionnaires qui continuent à utiliser un CB G1. Mais, à ce coefficient est attaché une courbe balistique bien particulière, et jusque 800m G1 ou G7 c'est kifkif, au de là ça se gâte, et les courbes divergent de façon assez fondamentale. Je poserai un thread sur ce problème.
 Sujets similaires
Sujets similaires» calcul du coefficient de stabilité miller
» probleme de math .....Et formule .....
» Formule excell 2010
» Influence du pas de rayure sur la stabilité gyroscopique...
» Stabilité gyroscopique et longueur du projectile
» probleme de math .....Et formule .....
» Formule excell 2010
» Influence du pas de rayure sur la stabilité gyroscopique...
» Stabilité gyroscopique et longueur du projectile
:: Le club-house :: La bibliothèque
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum







